Orde 2x2
JIka A dan B matriks bujur sangkar sedemikian rupa sehingga A B = B A = I , maka B disebut balikan atau invers dari A dan dapat dituliskan  ( B sama dengan invers A ). Matriks B juga mempunyai invers yaitu A maka dapat dituliskan
( B sama dengan invers A ). Matriks B juga mempunyai invers yaitu A maka dapat dituliskan  . Jika tidak ditemukan matriks B, maka A dikatakan matriks tunggal (singular). Jika matriks B dan C adalah invers dari A maka B = C.
. Jika tidak ditemukan matriks B, maka A dikatakan matriks tunggal (singular). Jika matriks B dan C adalah invers dari A maka B = C.
 ( B sama dengan invers A ). Matriks B juga mempunyai invers yaitu A maka dapat dituliskan
( B sama dengan invers A ). Matriks B juga mempunyai invers yaitu A maka dapat dituliskan  . Jika tidak ditemukan matriks B, maka A dikatakan matriks tunggal (singular). Jika matriks B dan C adalah invers dari A maka B = C.
. Jika tidak ditemukan matriks B, maka A dikatakan matriks tunggal (singular). Jika matriks B dan C adalah invers dari A maka B = C.Matriks A =
 dapat di-invers apabila ad - bc ≠ 0
dapat di-invers apabila ad - bc ≠ 0Dengan Rumus =

Apabila A dan B adalah matriks seordo dan memiliki balikan maka AB dapat di-invers dan 

Contoh 1: Matriks
-
- A =
 dan B =
dan B = 
- A =
-
- AB =

 =
=  = I (matriks identitas)
= I (matriks identitas)
- AB =
-
- BA =

 =
=  = I (matriks identitas)
= I (matriks identitas)
- BA =
Maka dapat dituliskan bahwa
 (B Merupakan invers dari A)
(B Merupakan invers dari A)Contoh 2: Matriks
-
- A =
 dan B =
dan B = 
- A =
-
- AB =

 =
= 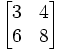
- AB =
-
- BA =

 =
= 
- BA =
Karena AB ≠ BA ≠ I maka matriks A dan matriks B disebut matriks tunggal.
Contoh 3: Matriks
-
- A =

- A =
Tentukan Nilai dari A-1
Jawab:

Contoh 4: Matriks
-
- A =
 , B =
, B =  , AB =
, AB = 
- A =
Dengan menggunakan rumus, maka didapatkan
-
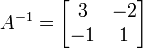 ,
, 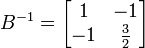 ,
, 
-

 =
= 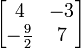
Ini membuktikan bahwa

Orde 3x3
-
- A =

- A =
kemudian hitung kofaktor dari matrix A
C11 = 12 C12 = 6 C13 = -16
C21 = 4 C22 = 2 C23 = 16
C31 = 12 C32 = -10 C33 = 16
menjadi matrix kofaktor
-
- adj(A) =

- adj(A) =
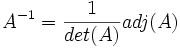
dengan metode Sarrus, kita dapat menghitung determinan dari matrix A


Penyelesaian Persamaan Linier Dengan Menggunakan Matriks (Orde 3x3)
Metode Cramer
jika Ax = b adalah sebuah sistem linear n yang tidak di ketahui dan det(A)≠ 0 maka persamaan tersebut mempunyai penyelesaian yang unik
Contoh soal: Gunakan metode cramer untuk menyelesaikan persoalan di bawah ini
-
- x1 + 2x3 = 6
-
- -3x1 + 4x2 + 6x3 = 30
-
- -x1 - 2x2 + 3x3 = 8
-
- A =
 b =
b = 
- A =
-
- A1 =
 A2 =
A2 =  A3 =
A3 = 
- A1 =
maka,
Jika A dapat di-invers, maka sesuai dengan teorema equivalent statements , maka R = I, jadi det(R) = 1 ≠ 0 dan det(A) ≠ 0. Sebaliknya, jika det(A) ≠ 0, maka det(R) ≠ 0, jadi R tidak memiliki baris yang nol. Sesuai dengan teorema R = I, maka A adalah dapat di-invers. Tapi jika matrix bujur sangkar dengan 2 baris/kolom yang proposional adalah tidak dapat diinvers.
Contoh Soal :

karena det(A) = 0. Maka A adalah dapat diinvers.
Sistem Linear Dalam Bentuk Ax = λx
dalam sistem aljabar linear sering ditemukanAx = λx ; dimana λ adalah skalarsistem linear tersebut dapat juga ditulis dengan λx-Ax=0, atau dengan memasukkan matrix identitas menjadi
(λI - A) x = 0contoh:
diketahui persamaan linear
x1 + 3x2 = λx1
4x1 + 2x2 = λx2
dapat ditulis dalam bentukyang kemudian dapat diubah
= λ
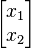
-
- A =
 dan x =
dan x =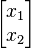
- A =
λ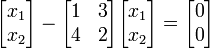
λ
sehingga didapat bentuk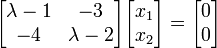
λ I - A =namun untuk menemukan besar dari λ perlu dilakukan operasi
det (λ I - A) = 0 ;λ adalah eigenvalue dari Adan dari contoh diperoleh
det (λ I - A) =atau λ^2 - 3λ - 10 = 0= 0
dan dari hasil faktorisasi di dapat λ1 = -2 dan λ2 = 5
dengan memasukkan nilai λ pada persamaan (λ I - A) x = 0, maka eigenvector bisa didapat bila λ = -2 maka diperoleh
dengan mengasumsikan x2 = t maka didapat x1 = t
x =
Sumber:
http://id.wikipedia.org/wiki/Aljabar_linear#Matriks_Balikan_.28Invers.29





Tidak ada komentar:
Posting Komentar